Anúncios
Fractals represent one of nature’s most mesmerizing mathematical phenomena, bridging the gap between art, science, and infinite complexity in ways that captivate both mathematicians and visual artists alike.
🌀 The Mathematical Poetry Behind Fractal Patterns
Anúncios
At the intersection of mathematics and visual splendor lies a universe of self-repeating patterns that challenge our understanding of dimension, scale, and beauty. Fractal aesthetics emerged from complex mathematical equations, yet their visual manifestations speak a universal language that transcends numerical formulas. These intricate structures appear everywhere in our natural world—from the branching of trees to the formation of coastlines, from the spiraling of galaxies to the delicate architecture of snowflakes.
The term “fractal” was coined by mathematician Benoit Mandelbrot in 1975, derived from the Latin word “fractus,” meaning broken or fractured. This naming convention perfectly captures the essence of these structures: geometric shapes that can be split into parts, each of which is a reduced-scale copy of the whole. This property, known as self-similarity, creates visual patterns that repeat at every magnification level, producing an infinite cascade of detail that never loses its complexity.
Anúncios
What makes fractal aesthetics particularly compelling is their ability to generate overwhelming visual complexity from relatively simple mathematical rules. The famous Mandelbrot Set, for instance, emerges from a straightforward iterative equation, yet produces an infinitely complex boundary with endless variations of spirals, tendrils, and miniature copies of itself. This paradox of simplicity generating complexity mirrors fundamental patterns found throughout nature and art.
Nature’s Blueprint: Fractal Geometry in the Living World 🍃
The natural world serves as the greatest exhibition of fractal aesthetics, demonstrating that these mathematical patterns are not merely abstract concepts but fundamental organizing principles of reality. Romanesco broccoli displays perhaps one of the most perfect examples of natural fractals, with its spiral arrangement repeating at multiple scales in a Fibonacci sequence. Each floret is a miniature version of the whole, creating a stunning logarithmic spiral that exemplifies mathematical beauty in edible form.
Trees and plants utilize fractal branching patterns for optimal efficiency in resource distribution. The vascular system of leaves follows fractal pathways to maximize surface area while minimizing distance, ensuring efficient nutrient transport. Similarly, our own circulatory and respiratory systems employ fractal architecture—blood vessels and bronchial tubes branch in self-similar patterns that optimize oxygen delivery throughout the body.
Rivers and their tributaries carve fractal drainage patterns into landscapes, creating networks that mathematicians can analyze using fractal dimensions. Coastlines present another fascinating example, as Mandelbrot himself discovered when investigating the question “How long is the coast of Britain?” The answer depends on measurement scale—the closer you look, the more detail emerges, and the measured length increases toward infinity.
Digital Canvas: Creating Fractal Art Through Technology 🎨
The digital revolution transformed fractal mathematics from theoretical abstraction into accessible visual art. Specialized software and algorithms now allow artists and enthusiasts to explore infinite mathematical landscapes, rendering these complex patterns in stunning colors and resolutions. Fractal generation software uses iterative processes to calculate and visualize these patterns, often employing escape-time algorithms that determine coloring based on how quickly points diverge under iteration.
Modern fractal artists manipulate parameters within these equations to produce unique aesthetic expressions. Variables like iteration depth, color mapping schemes, and transformation functions become the painter’s palette, offering infinite creative possibilities. The resulting artworks range from abstract psychedelic landscapes to photorealistic natural formations that blur the line between mathematical computation and organic beauty.
Three-dimensional fractal rendering has opened entirely new frontiers in visual complexity. Techniques like ray marching through distance-estimated fractal fields create volumetric structures of breathtaking intricacy. The Mandelbulb, a three-dimensional analog of the Mandelbrot Set, produces alien landscapes filled with recursive detail that seems both otherworldly and strangely familiar, echoing structures we observe in coral reefs and mineral formations.
The Color Symphony: Palettes That Bring Fractals to Life 🌈
Color plays a crucial role in fractal aesthetics, transforming mathematical calculations into emotionally resonant visual experiences. The coloring algorithms applied to fractals don’t merely represent mathematical values—they create mood, depth, and artistic interpretation. Smooth gradient techniques eliminate banding effects, producing fluid transitions that guide the viewer’s eye through increasingly detailed structures.
Artists often employ color palettes inspired by natural phenomena: sunset gradients, oceanic blues transitioning to deep purples, or volcanic reds fading into golden yellows. These choices aren’t arbitrary—they tap into our psychological associations with color, making mathematical abstractions feel warm, inviting, or dramatically intense. The strategic use of contrast highlights structural features, making certain fractal details pop against quieter background regions.
Some fractal artists experiment with unconventional coloring methods, including orbit traps that color points based on their proximity to specific shapes during iteration. This technique can produce striking effects where geometric forms appear embedded within fractal structures, creating layers of visual interest that reward prolonged contemplation.
Fractal Dimensions: Measuring the Immeasurable 📐
One of the most philosophically intriguing aspects of fractal aesthetics involves the concept of fractional dimensions. Classical geometry recognizes whole number dimensions: a line is one-dimensional, a plane is two-dimensional, and space is three-dimensional. Fractals, however, exist between these integer values, possessing fractal dimensions that quantify their complexity and space-filling properties.
The fractal dimension of a coastline, for example, typically falls between 1 and 2, reflecting how it’s more complex than a smooth line but doesn’t fully occupy two-dimensional space. This mathematical measure captures something profound about visual complexity—it quantifies our intuitive sense that certain patterns are “more intricate” than others. The higher the fractal dimension, the more space-filling and visually complex the structure appears.
This concept has practical applications beyond aesthetics. Scientists use fractal dimensions to analyze everything from market volatility to tumor boundaries, demonstrating how these mathematical tools help us understand complexity across diverse domains. In visual arts, understanding fractal dimensions helps artists gauge the perceived complexity of their compositions and balance intricate details with negative space.
Infinite Zoom: The Mesmerizing Journey Into Endless Detail 🔍
Perhaps the most captivating property of fractal aesthetics is the infinite zoom phenomenon—the ability to continuously magnify a fractal image and discover new details at every scale. This characteristic creates a unique viewing experience where exploration never ends and surprises always await deeper investigation. Fractal zoom videos have become popular online content, offering meditative journeys through mathematical landscapes that seem to extend forever.
The psychological impact of infinite zoom experiences taps into our innate curiosity and pattern-recognition instincts. As we descend into fractal depths, our minds constantly seek familiar shapes and structures within the chaos. This engagement creates an almost hypnotic effect, explaining why fractal visualizations are popular in meditation applications, music videos, and ambient visual displays.
Modern computational power enables real-time exploration of fractal spaces with remarkable precision. High-precision arithmetic allows zooming to astronomical depths—magnifications exceeding the ratio of the observable universe to a subatomic particle—while still revealing crisp, detailed structures. These extreme zooms demonstrate that mathematical patterns contain literally infinite information, a concept both beautiful and philosophically profound.
Architectural Inspirations: Fractals in Design and Structure 🏛️
The influence of fractal aesthetics extends beyond digital art into architecture and physical design. Many traditional architectural forms intuitively employed fractal principles long before mathematicians formalized the concept. Gothic cathedrals display self-similar details from overall structure down to individual ornamental elements. Hindu temples and Islamic geometric patterns demonstrate recursive complexity that creates visual richness and spiritual symbolism.
Contemporary architects increasingly incorporate explicit fractal design principles into buildings. These structures often feature improved environmental performance—fractal surfaces can optimize solar panel efficiency, improve acoustic properties, and enhance structural strength-to-weight ratios. The aesthetic appeal of fractal architecture also creates visually striking landmarks that harmonize with natural landscapes through shared geometric languages.
Urban planners recognize that cities themselves often develop fractal characteristics, with transportation networks, residential clustering, and commercial zones following self-similar patterns at different scales. Understanding these fractal growth patterns helps designers create more efficient, livable urban environments that accommodate organic expansion while maintaining functional coherence.
Psychedelic Connections: Fractals and Consciousness Exploration 🧠
The relationship between fractal patterns and altered states of consciousness has fascinated researchers and experiencers alike. Many individuals report seeing intricate geometric patterns, including fractal structures, during meditation, sensory deprivation, or psychedelic experiences. This connection suggests that fractal patterns might reflect fundamental organizing principles of neural processing or consciousness itself.
Neuroscience research indicates that brain activity exhibits fractal characteristics across temporal and spatial scales. Neural firing patterns, brainwave oscillations, and structural organization of neural networks all display fractal properties. This suggests our perception finds fractal patterns particularly resonant because they mirror our own cognitive architecture—we recognize in external fractals a reflection of internal mental processes.
Artists working in visionary and psychedelic genres frequently incorporate fractal aesthetics into their work, using these patterns to represent transcendent experiences or alternative perceptual states. The infinite complexity and self-similarity of fractals metaphorically express concepts like unity in diversity, the microcosm reflecting the macrocosm, and the interconnectedness of all scales of existence.
Musical Fractals: When Sound Meets Self-Similarity 🎵
Fractal principles extend beyond visual realms into sonic territories, where composers and sound designers create musical structures with self-similar properties. Fractal music employs algorithms that generate melodies, rhythms, or harmonic progressions that repeat at different time scales, creating compositions with recognizable motifs that recur in varied forms throughout a piece.
Classical composers like Bach intuitively created fractal-like structures through techniques such as fugues and canons, where melodic themes repeat at different pitches and speeds. Contemporary electronic musicians explicitly employ fractal generation algorithms, producing soundscapes that mirror the infinite complexity of visual fractals. This approach creates music that feels both unpredictable and structurally coherent—familiar patterns emerge within apparent chaos.
The connection between visual and musical fractals creates opportunities for synesthetic art experiences. Audiovisual performances synchronize fractal imagery with fractal-inspired soundscapes, producing multisensory immersions where mathematical patterns manifest simultaneously through sight and sound. These experiences demonstrate the universality of fractal patterns across different perceptual modalities.
Therapeutic Applications: Healing Through Pattern and Complexity ✨
The calming effect of observing fractal patterns has led to therapeutic applications in stress reduction and mental health treatment. Research indicates that viewing natural fractal patterns reduces physiological stress markers, including lowered blood pressure and decreased cortisol levels. This response may explain humanity’s deep-seated attraction to natural environments, which are rich in fractal structures.
Art therapy practitioners incorporate fractal creation and observation into treatment protocols for anxiety, PTSD, and depression. The process of generating fractal art through simple iterative actions provides a meditative focus, while the resulting complex beauty offers a sense of accomplishment and aesthetic satisfaction. The non-judgmental nature of mathematical beauty—fractals are neither good nor bad, simply are—creates a safe space for emotional processing.
Virtual reality applications now offer immersive fractal environments for meditation and therapeutic purposes. Users can navigate through three-dimensional fractal landscapes, experiencing the sense of infinite space and endless detail that promotes mindful presence and stress relief. These digital nature experiences leverage fractal aesthetics to provide restoration benefits similar to spending time in natural settings.
Future Horizons: Where Fractal Aesthetics Meet Emerging Technologies 🚀
Artificial intelligence and machine learning are opening new frontiers in fractal art creation. Neural networks trained on fractal datasets can generate novel patterns that blend learned aesthetic principles with mathematical precision. These AI-assisted tools democratize fractal art creation, allowing individuals without deep mathematical knowledge to explore and manipulate fractal aesthetics intuitively.
Quantum computing promises to revolutionize fractal rendering capabilities, potentially enabling real-time generation of ultra-high-resolution fractal animations with unprecedented depth and complexity. As computational power continues expanding, the boundary between mathematical calculation and creative expression grows increasingly permeable, suggesting future art forms we can barely imagine today.
Augmented reality applications will likely bring fractal aesthetics into our daily environments, overlaying mathematical beauty onto physical spaces. Imagine walking through a forest while AR glasses reveal the hidden fractal geometries in tree branching, or viewing architecture enhanced with dynamically generated fractal ornamentation that responds to viewer movement and environmental conditions.
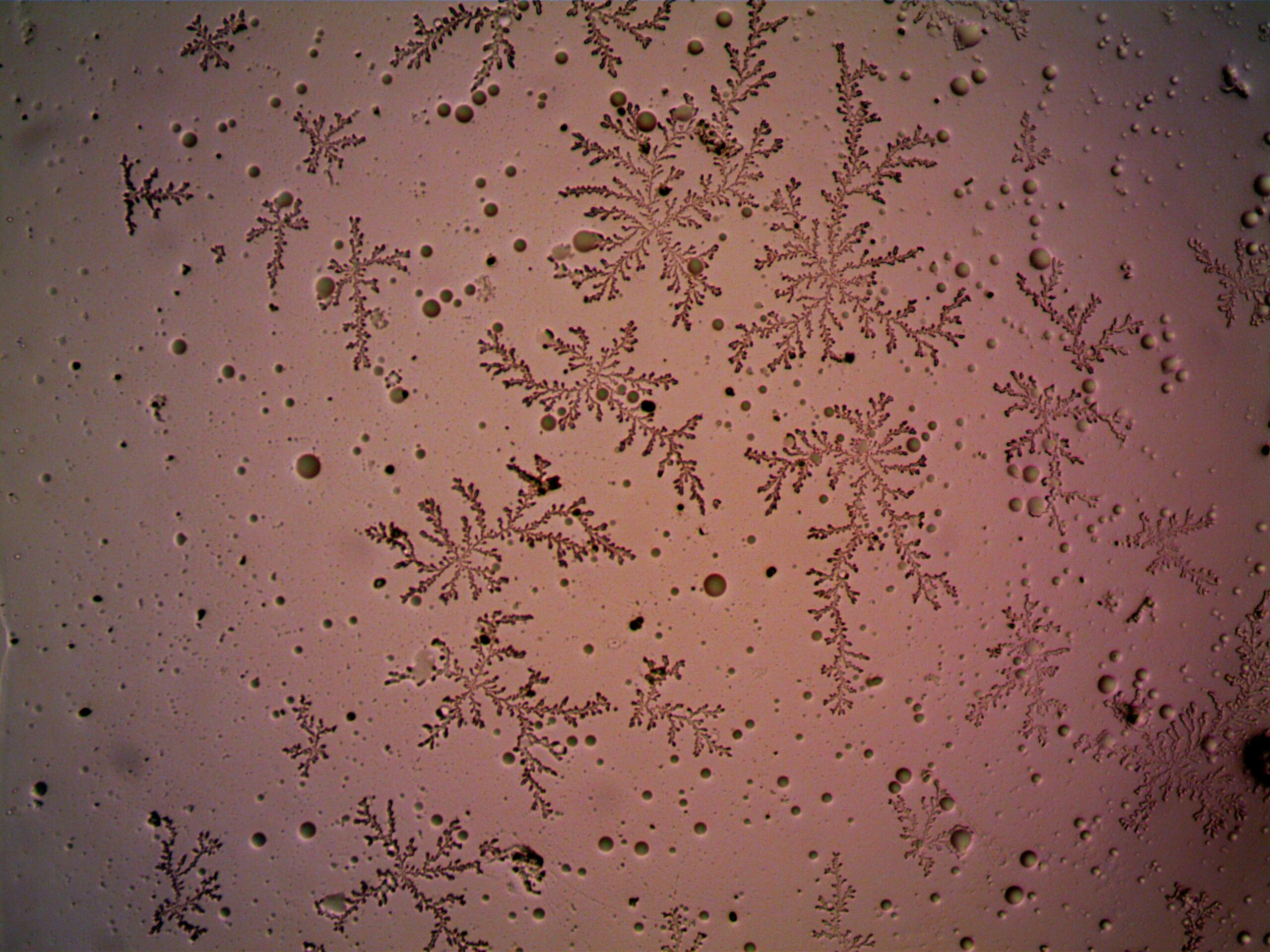
The Universal Language of Self-Similarity 🌍
Fractal aesthetics transcend cultural boundaries, offering a visual language understood across different societies and backgrounds. The mathematical universality of fractal patterns means they appear in diverse cultural traditions—from African textile designs to Celtic knots, from Indigenous Australian art to Asian architectural motifs. This global presence suggests fractal patterns tap into fundamental human perceptual preferences shaped by our evolutionary relationship with natural environments.
The educational value of fractals lies in their ability to make abstract mathematics tangible and beautiful. Students who might find traditional geometry dry often become engaged when exploring fractal patterns, discovering that mathematics can produce stunning visual results. This pedagogical power makes fractals valuable tools for STEAM education, bridging analytical and creative thinking.
As we continue unveiling the beauty of fractal aesthetics, we discover not merely mathematical curiosities but fundamental patterns that connect mathematics, art, nature, and consciousness. These infinite structures remind us that complexity and beauty often emerge from simple rules applied recursively—a principle as relevant to personal growth and creative endeavors as to mathematical exploration. The visual symphony of fractals plays on, inviting endless exploration into the elegant complexity that underlies our universe.
